시간 복잡도(Big-O) 계산하기, Worst Accepted Algorithm

왜 Big-O 표기법으로 시간 복잡도를 계산하지?

 

Big-O 표기법은 최대 차항만 계수 없이 표기하면 되기 때문에 사용하기 간편하고, 알고리즘의 최악의 경우를 의미해서 평균과 가까운 결과를 예측 할 수 있기 때문입니다.

 

그래서 Big-O 복잡도가 무엇이 있는가

 

https://joshuajangblog.wordpress.com/2016/09/21/time_complexity_big_o_in_easy_explanation/

 

 

node.js는 (싱글 스레드인 이벤트 루프에서 기본적인 코드를 처리하므로) 싱글 스레드죠? 그렇기에 복잡도가 높은 코드를 처리하면서 blocking되는 현상을 막아야 합니다. 때문에 코드를 비동기적으로 짜야 하는 것이죠.

 

그런데 웹 개발을 하다보면 솔직히 O(n) 정도의 복잡도 이상의 코드를 보기가 힘듭니다. (제가 허접해서 그런 걸 수도 있습니다.)

 

js 개발자는 이중 map, filter를 돌려 O(n^2)의 복잡도를 가진 코드를 작성하게 될 때도 있지만 대부분 n이 아주 작을 때, 구체적으로는 10을 넘어가지 않는 수준이라 복잡도 자체를 무시할 수 있는 수준이거나, (아주 드물긴하지만) 그렇지 않은 경우에는 리팩토링을 해서 다른 방식으로 코드를 작성하게 됩니다.

 

n 자체가 깡으로 높을 때는 worker_threads를 통해 멀티 쓰레딩으로 처리합니다. 아래처럼 말이죠.

darrengwon.tistory.com/954

Thread Pool을 활용해 멀티 쓰레딩로 고비용 연산 처리하기

 

그런데 멀티 쓰레딩을 함부로 쓰면 Worker를 생성하고 소통하는 비용이 더 클 수 있습니다.

일반적으로 N의 갯수에 따라 용납되는 알고리즘을 따져보고 사용합시다.

10개면 팩토리얼도 된다네요 ㅋㅋㅋ

 

https://www.hackerearth.com/practice/basic-programming/complexity-analysis/time-and-space-complexity/tutorial/

 

 

 

Big-O 계산 어떻게 함?

 

몇번 코드가 반복되는지를 체킹하면 됩니다.

 

1)

int sum = 0;
for(int i=0; i<N; i++)
    for(int j=0; j<i; j++)
        sum += j;

 

N번 만큼 i가 도는데 i 마다 j가 i만큼 돕니다. 따라서 O(N^2) 입니다.

n이 웬만큼 작지 않은 이상 이중 map, filter 돌리지 말라는 이유죠. 

위 표에 따르면 O(N^2)은 10,000개 까지는 써도 된다는데 Node.js는 조심해야 합니다... 그리고 아무리 용납된다고 하더라도 그렇게 짤 이유가 전혀 없습니다.

 

2)

int sum = 0;
for(int i=N; i>0; i/=2)
    for(int j=0; j<i; j++)
        sum += j;

 

N이 10일때

 

i) i = 10 => j= 0, 1 2, 3, 4, 5, 6, 7, 8, 9

ii) i = 5 => j = 1, 2, 3, 4

iii) i = 2 => j = 1

iiii) i = 1 => j = 0

 

꼴로 움직이므로 N/2 만큼 도는 것을 알 수 있습니다. 

Big-O는 최고 차항만 따지니까 O(N/2) 같은 건 없죠. O(N)로 치면 됩니다.

 

 

시간 복잡도에 따른 실제 퍼포먼스 차이를 살펴보자

 

addAll은 O(n)이고

addAll2는 O(1)이다.

function addAll(n) {
  let sum = 0;
  for(let i = 0; i < n; i++) {
    sum += i;
  }
  return sum;
}

function addAll2(n) {
  return n * (n + 1) / 2;
}

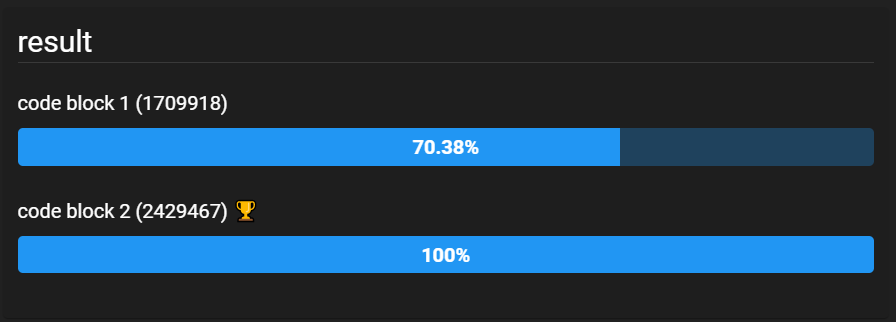
결과는 다음과 같다.

2번 block 즉, addAll2가 성능이 좋다는 것을 알 수 있다.

 

js 메서드 성능 측정은 앞으로 아래를 써보자.

jsben.ch/

JSBEN.CH Performance Benchmarking Playground for JavaScript

 

 

 

참고 문서)

 

www.hackerearth.com/practice/basic-programming/complexity-analysis/time-and-space-complexity/tutorial/

Time and Space Complexity Tutorials & Notes | Basic Programming | HackerEarth

medium.com/humanscape-tech/%EC%BD%94%EB%93%9C%EC%9D%98-%EC%8B%9C%EA%B0%84-%EB%B3%B5%EC%9E%A1%EB%8F%84-%EA%B3%84%EC%82%B0%ED%95%98%EA%B8%B0-b67dd8625966

코드의 시간 복잡도 계산하기