svg path에 대해 어느 정도 알아둬야 합니다.
svg element : 기본 모양들
developer.mozilla.org/ko/docs/Web/SVG/Element SVG element reference - SVG | MDN developer.mozilla.org 기본 모양들 아래 외에 storke 등의 스타일링을 추가해줄 수 있습니다. path를 잘 쓰는 방법은 d 속성..
darrengwon.tistory.com
Line graph
line 객체를 들어서 path attr의 d로 넣어주면 됩니다.
아래 코드의 경우 (0, 24) (50, 30) (100, 45) (150, 70) (200, 26) 을 line으로 연결한 결과를 그리겠군요.
import React, { useRef, useEffect, useState } from "react";
import { select, line } from "d3";
function App() {
const [data, setData] = useState([24, 30, 45, 70, 26]);
const svgRef = useRef(null);
useEffect(() => {
const svg = select(svgRef.current); // selection 객체
// line 객체를 만들자
const myLine = line()
.x((value, index) => index * 50)
.y((value) => value);
svg
.selectAll("path")
.data([data])
.join((enter) => enter.append("path"))
.attr("d", (value) => myLine(value))
.attr("fill", "none")
.attr("stroke", "red");
}, [data]);
return (
<>
<svg
ref={svgRef}
xmlns="http://www.w3.org/2000/svg"
width="300"
height="300"
viewBox="0 0 300 300"
version="1.1"
></svg>
</>
);
}
export default App;
결과로 아래와 같은 결과를 얻습니다.
path를 사용해보셨으면 알겠지만 웹에선 y축 좌표가 반대입니다.

반대라서 마음에 안들고 무엇보다 직관적이지 않습니다.
반대이니 음의 방향으로 반전해주고 적절한 크기 만큼 y축으로 평행이동 시켜줍시다. (중학교 수학입니다)
svg viewBox의 크기를 저는 300을 잡았으므로 300만큼 주겠습니다.
// line 객체를 만들자
const myLine = line()
.x((value, index) => index * 50)
.y((value) => 300 - value);
직관적으로 변한 것을 확인할 수 있습니다.

Curved Line graph
github.com/d3/d3-shape/blob/v2.0.0/README.md#curves
d3/d3-shape
Graphical primitives for visualization, such as lines and areas. - d3/d3-shape
github.com
위 코드를 그대로 curved로 바꿔봅시다. path의 C나 S를 이용할 필요 없이 D3에서 제공해주는 curve 메서드와 curve 객체를 사용하면 됩니다.
import { select, line, curveBasis } from "d3";
// line 객체를 만들자
const myLine = line()
.x((value, index) => index * 50)
.y((value) => 300 - value)
.curve(curveBasis);

사용할 수 있는 curve가 무엇이 있는지 index.d.ts를 뒤져봤습니다.
d3-shape의 index.d.ts 부분을 보시면 Curve Factories 부분에 curve generator들을 살펴보실 수 있습니다.
양이 꽤 많은데 기본적인 것만 살펴보면 다음과 같은 것들이 있습니다.
CurveFactory를 상속 받는 curve
curveBasis
curveBasisClosed
curveBasisOpen
CurveCardinalFactory를 상속받는 curve
curveCardinal
curveCardinalClosed
curveCardinalOpen
CurveCatmullRomFactory를 상속받는 curve
curveCatmullRom
curveCatmullRomClosed
curveCatmullRomOpen
...etc
일정한 규칙을 확인할 수 있는데 공식문서에 따르면 다음과 같습니다.

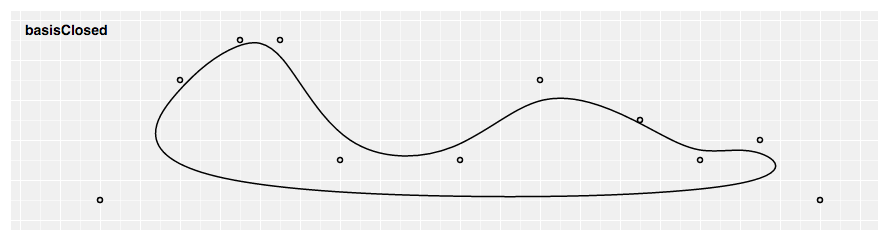
Produces a closed cubic basis spline(basis spline은 b-spline 이라고도 불리웁니다) using the specified control points. When a line segment ends, the first three control points are repeated, producing a closed loop with C2 continuity.

Produces a cubic basis spline using the specified control points. Unlike basis, the first and last points are not repeated, and thus the curve typically does not intersect these points.
Spline, C2 continuity?
curve가 예쁘니까 curve를 쓰자! 라고 접근하기에는 그 배후에 놓인 수학 개념들을 무시할수가 없습니다.
문과지만 찾아보았습니다.
* 어떻게 직선을 부드러운 곡선으로 그리는가? => spline 보간법
helloworldpark.github.io/jekyll/update/2017/02/04/Spline.html
스플라인 보간법 - 점을 부드럽게 잇기
이 페이지는 이 페이지의 내용을 기반으로 작성되었으며, 구현은 여기를 참고하시면 됩니다. 그리고 수식이 보기 싫으신 분은 맨 밑의 그래프만 보시면 됩니다. 점을 부드럽게 잇기 아래 그림과
helloworldpark.github.io
결론적으로, 부드럽다는 것은 이어져있어야 한다. (연속함수)
단순히 이어진 것을 넘어 기울기(미분값)까지도 부드러워야 한다 => 1계 미분 연속이어야 함
기울기가 변하는 정도(곡률)도 부드러워야 한다 => 2계 미분 연속이어야 함
따라서 부드러운 곡선은 2번 미분하여 연속인 함수여야 한다.
직선을 부드러운 곡선 함수로 보간하는 알고리즘은 Cubic Spline Interpolation 이라고 합니다.
* spline은 무엇인가.
결론적으로, 다항식 곡선 = 스플라인(spline) 입니다.
곡선(면)설계, 애니메이션 경로 설계 등에 이용됩니다.
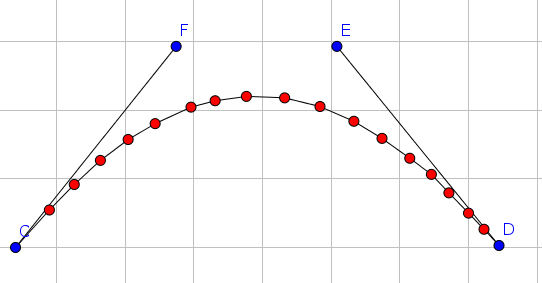
각각의 점들이 제어점(CP: Control Points)이고
각 제어점을 부드럽게 연결하지 않고 직선적으로 연결한 것을 컨벡스 헐(Convex Hull) 이라고 부르더군요.
스플라인이 컨벡스 헐 내부에만 존재할 경우 진동(Oscillation)이나 이탈(Overshoot)이 방지된다고 합니다.
수학을 떠나 직관적으로 생각해보면, 이는 자명하다고 받아들일 수 있는 정도의 지식입니다.

* 스플라인의 연속성(Continuity)
xxxClosed가 붙은 류의 그래프들은 producing a closed loop with C2 continuity. 한다고 하는데, 여기서 C2 연속성은
들어오는 기울기의 변화율(2차 미분 계수, 기울기의 기울기)이 나가는 기울기의 변화율과 같은 것을 의미합니다.
고등학교 때 수학을 생각해보면, 특정 함수가 연속이냐 아니냐를 판단하기 위해 들어오는(좌측 극한값)과 나가는 값(우측 극한값)을 비교했는데 그 개념을 2차 미분계수에 적용한 것이라고 이해하면 되겠습니다.
* spline에 대한 더 많은 정보는 아래 정보를 참고하시면 되겠습니다.
ivis.kr/images/0/07/14_%EC%8A%A4%ED%94%8C%EB%9D%BC%EC%9D%B8.pdf
'📈 js 그래픽 > react + d3.js' 카테고리의 다른 글
| React + D3.js (5) Animation (0) | 2021.01.18 |
|---|---|
| React + D3.js (4) Bar Chart (1) | 2021.01.18 |
| React + D3.js (3) Axes and Scales (0) | 2021.01.17 |
| React + D3.js (1) D3 소개와 React와 접목 (1) | 2021.01.17 |
